ДДП — различия между версиями
Dima (обсуждение | вклад) |
Admin (обсуждение | вклад) |
||
| (не показано 8 промежуточных версий 3 участников) | |||
| Строка 1: | Строка 1: | ||
| − | ''' | + | '''БАЗОВЫЕ ВОПРОСЫ ДИСКОНТИРОВАНИЯ ДЕНЕЖНЫХ ПОТОКОВ''' |
| − | ''' | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
'''I.''' В общем виде, под дисконтированием понимается «определение текущего | '''I.''' В общем виде, под дисконтированием понимается «определение текущего | ||
| Строка 56: | Строка 26: | ||
Рис. 1. Графическая модель процесса дисконтирования | Рис. 1. Графическая модель процесса дисконтирования | ||
| − | По своей экономической сущности ставка дисконтирования отражает ''скорость изменения стоимости денег во времени''. Отметим, что проблематика обоснования величины ставки дисконтирования, в том числе, сравнительная характеристика существующих методик, заслуживает отдельного полноценного исследования и лежит за пределами тематики настоящей статьи. | + | По своей экономической сущности ставка дисконтирования отражает ''скорость изменения стоимости денег во времени''. Отметим, что проблематика обоснования величины ставки дисконтирования, в том числе, сравнительная характеристика существующих методик, заслуживает отдельного полноценного исследования и лежит за пределами тематики настоящей статьи.<br /> |
| + | <br /> | ||
'''II.''' Формула (1) подразумевает, что денежный поток возникнет в конце периода времени ''t''. В реальных общественно-экономических системах такая ситуация достаточно редка, поскольку как поступления, так и оттоки денежных средств распределены во времени [3]. Причинами распределенности денежных потоков могут являться как достаточная продолжительность периода времени ''t'', так и специфика конкретного доходогенерирующего актива. Например, у предприятий общественного питания поток доходов и расходов обычно равномерней, чем у предприятий строительной отрасли. | '''II.''' Формула (1) подразумевает, что денежный поток возникнет в конце периода времени ''t''. В реальных общественно-экономических системах такая ситуация достаточно редка, поскольку как поступления, так и оттоки денежных средств распределены во времени [3]. Причинами распределенности денежных потоков могут являться как достаточная продолжительность периода времени ''t'', так и специфика конкретного доходогенерирующего актива. Например, у предприятий общественного питания поток доходов и расходов обычно равномерней, чем у предприятий строительной отрасли. | ||
| Строка 72: | Строка 43: | ||
Рис. 2. Графическая модель дисконтирования равномерно распределенных потоков | Рис. 2. Графическая модель дисконтирования равномерно распределенных потоков | ||
| − | Из выражений (1) и (2) также может быть выведена формула дисконтирования на начало периода – в ней показателем степени будет «t – 1». | + | Из выражений (1) и (2) также может быть выведена формула дисконтирования на начало периода – в ней показателем степени будет «t – 1».<br /> |
| + | <br /> | ||
'''III.''' Выражения (1) и (2) можно рассматривать как первую и вторую итерацию повышения точности ЭММ ДДП. Следующим этапом приближения модели ДДП к реальным общественно-экономическим системам является использование плавающей (переменной) ставки дисконтирования. Как известно, основными факторами, определяющими величину ставки дисконтирования, являются инфляция, упущенная выгода и риск. В реальных проектах все указанные величины изменяются с течением времени, что, естественно, должно найти отражение и в изменении величины ставки дисконтирования. | '''III.''' Выражения (1) и (2) можно рассматривать как первую и вторую итерацию повышения точности ЭММ ДДП. Следующим этапом приближения модели ДДП к реальным общественно-экономическим системам является использование плавающей (переменной) ставки дисконтирования. Как известно, основными факторами, определяющими величину ставки дисконтирования, являются инфляция, упущенная выгода и риск. В реальных проектах все указанные величины изменяются с течением времени, что, естественно, должно найти отражение и в изменении величины ставки дисконтирования. | ||
| Строка 195: | Строка 167: | ||
| − | Например, при годовой ставке дисконтирования в размере 20% расчет величины месячной ставки по формуле (9) даст результат в размере 1,531%, а по формуле (10) – в размере 1,667%. Данное расхождение в ряде ситуаций может быть некритичным (не оказывающим существенное влияние на итоговую величину стоимости). | + | Например, при годовой ставке дисконтирования в размере 20% расчет величины месячной ставки по формуле (9) даст результат в размере 1,531%, а по формуле (10) – в размере 1,667%. Данное расхождение в ряде ситуаций может быть некритичным (не оказывающим существенное влияние на итоговую величину стоимости).<br /> |
| + | <br /> | ||
'''IV.''' В заключение статьи рассмотрим вопрос дисконтирования стоимости реверсии. Обычно под реверсией (синонимы «терминальная стоимость», «продленная стоимость») понимаются поступления от продажи объекта оценки в конце прогнозного периода, иногда данным термином называют капитализированную величину денежных потоков постпрогнозного периода. В оценочном сообществе и методической литературе существует дискуссия относительно обоснования периода дисконтирования реверсии при определении ее текущей стоимости. В связи с этим отметим следующее: | '''IV.''' В заключение статьи рассмотрим вопрос дисконтирования стоимости реверсии. Обычно под реверсией (синонимы «терминальная стоимость», «продленная стоимость») понимаются поступления от продажи объекта оценки в конце прогнозного периода, иногда данным термином называют капитализированную величину денежных потоков постпрогнозного периода. В оценочном сообществе и методической литературе существует дискуссия относительно обоснования периода дисконтирования реверсии при определении ее текущей стоимости. В связи с этим отметим следующее: | ||
| Строка 215: | Строка 188: | ||
Для типичных объектов коммерческой недвижимости в российских городах - милионниках, для эксплуатации которых не требуется проведение значительных строительных мероприятий, различие в итоговой величине стоимости при разных периодах дисконтирования реверсии (см. п. 2 и 3) составит около 3-4%(отметим, что это влияние на результат только одного из подходов к оценке).<br /> | Для типичных объектов коммерческой недвижимости в российских городах - милионниках, для эксплуатации которых не требуется проведение значительных строительных мероприятий, различие в итоговой величине стоимости при разных периодах дисконтирования реверсии (см. п. 2 и 3) составит около 3-4%(отметим, что это влияние на результат только одного из подходов к оценке).<br /> | ||
| − | Учитывая вышеизложенное, в отчетах об оценке целесообразно в явном виде указывать: модель доходного подхода подразумевает, что объект оценки будет продан в конце прогнозного периода – период дисконтирования реверсии совпадает с продолжительностью прогнозного периода. | + | Учитывая вышеизложенное, в отчетах об оценке целесообразно в явном виде указывать: модель доходного подхода подразумевает, что объект оценки будет продан в конце прогнозного периода – период дисконтирования реверсии совпадает с продолжительностью прогнозного периода.<br /> |
| + | |||
Положения, представленные в настоящей статье, преследуют практическую цель повышения уровня усвоения учебного материала обучающихся по дисциплинам оценочного и управленческого пула, а также повышение профессионального уровня оценщиков.<br /> | Положения, представленные в настоящей статье, преследуют практическую цель повышения уровня усвоения учебного материала обучающихся по дисциплинам оценочного и управленческого пула, а также повышение профессионального уровня оценщиков.<br /> | ||
| + | <br /> | ||
| − | + | [[Category:Основы]] | |
| − | |||
| − | |||
Текущая версия на 13:16, 31 января 2018
БАЗОВЫЕ ВОПРОСЫ ДИСКОНТИРОВАНИЯ ДЕНЕЖНЫХ ПОТОКОВ
I. В общем виде, под дисконтированием понимается «определение текущего эквивалента денежных средств, ожидаемых к получению в определенный момент в будущем» [1]. В ряде случаев, дисконтированием называют процесс приведения ретроспективных денежных потоков на текущую дату, хотя в такой ситуации более уместно говорить про индексирование.
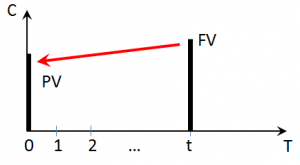
Ниже представлены исходная формула дисконтирования по сложному проценту [2], а также ее графическая интерпретация (рис. 1):
(1)
где: PV – текущая стоимость, ден. ед.;
FV – будущая стоимость, ден. ед.;
i – ставка дисконтирования, доли ед./период;
t – количество периодов с даты оценки (даты, к которой приводятся стоимости потоков) до даты возникновения потока, ед.
Рис. 1. Графическая модель процесса дисконтирования
По своей экономической сущности ставка дисконтирования отражает скорость изменения стоимости денег во времени. Отметим, что проблематика обоснования величины ставки дисконтирования, в том числе, сравнительная характеристика существующих методик, заслуживает отдельного полноценного исследования и лежит за пределами тематики настоящей статьи.
II. Формула (1) подразумевает, что денежный поток возникнет в конце периода времени t. В реальных общественно-экономических системах такая ситуация достаточно редка, поскольку как поступления, так и оттоки денежных средств распределены во времени [3]. Причинами распределенности денежных потоков могут являться как достаточная продолжительность периода времени t, так и специфика конкретного доходогенерирующего актива. Например, у предприятий общественного питания поток доходов и расходов обычно равномерней, чем у предприятий строительной отрасли.
Отметим, что все модели в целом, и экономико-математическая модель (ЭММ) дисконтирования в частности, являются упрощением моделируемого объекта или системы. При более глубоком анализе может оказаться, что при относительно равных ежедневных доходах в течение месяца у предприятий общественного питания наблюдаются значительные колебания доходов в течение одного дня – например, в связи с разным уровнем загрузки в утренние и вечерние часы, наличием комплексных предложений (бизнес-ланчей), цена элементов которых определяется с дисконтом относительно стандартного меню. Таким образом, с позиции методологии, при целевой установке на повышение точности расчетной модели дисконтирование должно проводиться при минимально возможном периоде (шаге) дисконтирования. В реальной оценочной практике, наиболее часто периодами дисконтирования являются год, полугодие, квартал и месяц – это позволяет привести соотношение «трудоемкость/точность» к уровню, адекватному решаемой задаче.
При условно равномерном распределении денежных потоков в течение интервала (0; t) формула (1) преобразуется следующим образом:
(2)
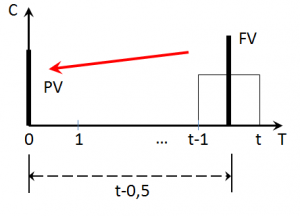
Чем ближе к дате оценки часть денежного потока, тем ближе период дисконтирования к t; чем ближе часть денежного потока к моменту времени t-1 , тем ближе период дисконтирования к t-1; средним арифметическим периодом дисконтирования является t-0,5. Графическая интерпретация выражения (2) показана на рис. 2:
Рис. 2. Графическая модель дисконтирования равномерно распределенных потоков
Из выражений (1) и (2) также может быть выведена формула дисконтирования на начало периода – в ней показателем степени будет «t – 1».
III. Выражения (1) и (2) можно рассматривать как первую и вторую итерацию повышения точности ЭММ ДДП. Следующим этапом приближения модели ДДП к реальным общественно-экономическим системам является использование плавающей (переменной) ставки дисконтирования. Как известно, основными факторами, определяющими величину ставки дисконтирования, являются инфляция, упущенная выгода и риск. В реальных проектах все указанные величины изменяются с течением времени, что, естественно, должно найти отражение и в изменении величины ставки дисконтирования.
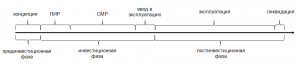
Наглядной иллюстрацией указанных изменений служит реализация полноценного девелоперского проекта, предусматривающего как создание объекта недвижимости, так и его последующую эксплуатацию. Схематичная разбивка жизненного цикла девелоперского проекта на этапы и фазы показана на рис. 3:
Рис. 3. Жизненный цикл девелоперского проекта
Наибольшие риски обычно соответствуют инвестиционной фазе (более конкретно – этапу строительно-монтажных работ, СМР), поскольку при выходе из проекта в указанный момент времени девелопер понесет наибольшие потери. Объем потерь будет определяться как суммарным размером фактически понесенных издержек, так и низкой ликвидностью объекта недвижимости на ранних этапах его создания.
Формула дисконтирования по переменной ставке имеет следующий вид:
(3)
где: – ставка дисконтирования в интервал времени с
до
, доли ед./период.
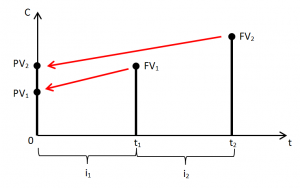
Для выведения выражения (3) из (1) и (2) рассмотрим пример, когда дисконтированию подлежат денежные потоки двух периодов, каждый из которых характеризуется различной величиной ставки дисконтирования – рис. 4 и табл. 1 (для наглядности расчеты выполним на конкретных цифрах).
Рис. 4. Графическая интерпретация условий примера
Таблица 1. Исходные условия примера
| Показатель | Значение |
| |
150 |
| |
200 |
| Продолжительность периодов |
1 |
| |
20 |
| |
15 |
Текущая стоимость потока FV1 определяется по формуле (1):
(4)
Дробь в квадратных скобках из выражения (4) имеет название «дисконтный множитель». Экономический смысл данного параметра заключается в том, что он показывает соотношение текущей и будущей стоимостей денежного потока. Соответственно, дисконтный множитель для периода времени показывает отношение текущей стоимости денежных потоков, возникших в момент времени
, к их будущей стоимости на момент времени
.
Процесс дисконтирования потока для наглядности разобьём на два этапа:
• приведение с момента времени к моменту времени
;
• приведение с момента времени к начальному моменту времени (дате оценки).
Приведение потока к моменту времени
также выполняется по формуле (1):
(5)
Для приведения полученной в выражении (5) величины к начальному моменту времени ее необходимо умножить на дисконтный множитель для периода времени , полученный в формуле (4):
(6)
Из выражений (5) и (6) имеем:
(7)
Полученное выражение (7) соответствует исходному (3) при двух периодах дисконтирования.
Процесс дисконтирования денежных потоков на середину периода по плавающей ставке выполняется по следующей формуле:
(8)
Графическая интерпретация формулы (8) представлена на рис. 5, практическая реализация показана в табл. 2.
Рис. 5. Графическая модель дисконтирования по переменной ставке на середину периода
Таблица 2. ДДП по плавающей ставке на середину периода
| Показатель | 1 год | 2 год | 3 год | 4 год |
| Ставка дисконтирования, %/год | 20 | 20 | 15 | 15 |
| Период дисконтирования, лет | 0,5 | 1,5 | 2+0,5 | 2+1,5 |
| Дисконтный множитель | 0,913 | 0,761 | 0,648 | 0,563 |
| Комментарий | |
|
|
Отметим, что часто возникает необходимость перевода, например, годовой ставки дисконтирования в квартальную. Зависимость между ставками дисконтирования для различных по продолжительности периодов времени имеет следующий вид:
(9)
где T – бóльший по продолжительности период времени;
t – меньший по продолжительности период времени.
Выражение учитывает, что обесценивание происходит по сложному проценту. Практической реализацией выражения (9) являются соотношения, показанные в табл. 3:
Таблица 3. Соотношение ставок дисконтирования для различных периодов
| Ставка дисконтирования | Формула расчета из годовой ставки дисконтирования (tгод) |
| Месячная | |
| Квартальная | |
| Полугодовая | |
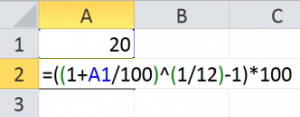
Перевод годовой ставки дисконтирования в размере 20% в ежемесячную в программе Microsoft Excel может быть выполнен следующим способом:
Отметим, что при невысоких требованиях к точности расчета можно пренебречь тем, что обесценивание происходит по сложному проценту. В этом случае перевод ставки может выполняться по следующему соотношению (предполагает, что обесценивание происходит по простому проценту):
(10)
Например, при годовой ставке дисконтирования в размере 20% расчет величины месячной ставки по формуле (9) даст результат в размере 1,531%, а по формуле (10) – в размере 1,667%. Данное расхождение в ряде ситуаций может быть некритичным (не оказывающим существенное влияние на итоговую величину стоимости).
IV. В заключение статьи рассмотрим вопрос дисконтирования стоимости реверсии. Обычно под реверсией (синонимы «терминальная стоимость», «продленная стоимость») понимаются поступления от продажи объекта оценки в конце прогнозного периода, иногда данным термином называют капитализированную величину денежных потоков постпрогнозного периода. В оценочном сообществе и методической литературе существует дискуссия относительно обоснования периода дисконтирования реверсии при определении ее текущей стоимости. В связи с этим отметим следующее:
1. Единого правила определения периода дисконтирования реверсии нет, поскольку он, как и при определении текущей рыночной стоимости денежных потоков прогнозного периода, зависит от характера поступления денежных потоков.
2. В большинстве случаев реверсия дисконтируется с конца прогнозного периода, например:
2.1. Если в доходном подходе к оценке моделируется продажа объекта оценки в конце прогнозного периода, а стоимость продажи определена не методом капитализации (величина реверсии определена индексацией результатов оценки по сравнительному подходу, погашение номинальной стоимости облигации в конце периода ее размещения и пр.).
Существует точка зрения, что в описанной ситуации период дисконтирования должен определяться как прогнозный период плюс период экспозиции объекта оценки. В обоснование подобной позиции приводится аргумент, что собственник объекта оценки, решив продать его в конце прогнозного периода, вынужден будет искать покупателя в течение рыночного периода экспозиции. Подобная точка зрения ошибочна по следующей причине. При определении стоимости моделируется поведение типичных субъектов (например, при определении рыночной стоимости – поведение типичных покупателя и продавца на соответствующем сегменте рынка). Эффективный собственник объекта, планируя продать объект оценки в конце прогнозного периода и зная, что для объекта оценки характерен определенный период экспозиции, начнет искать потенциального покупателя еще до окончания прогнозного периода. Сделка по продаже объекта оценки будет заключена таким образом, что права на объект перейдут к новому собственнику в тот момент, когда закончатся права и обязательства предыдущего собственника, связанные с получение доходов в прогнозном периоде. Даже если покупатель не найден до конца предполагаемого прогнозного периода (предполагаемой даты окончания получения доходов от использования объекта оценки), стандартной рыночной практикой является продолжение эксплуатации объекта оценки параллельно с поиском покупателя – разрыв между концом прогнозного периода и датой возникновения реверсии отсутствует.
2.2. Если реверсия определена методом капитализации денежного потока первого года постпрогнозного периода, в котором коэффициент капитализации определен методом рыночной экстракции.
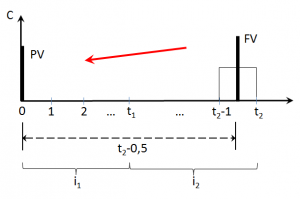
3. В некоторых специфических ситуациях период дисконтирования реверсии может определяться как продолжительность прогнозного периода минус 0,5 [4]. Отметим, что в таком случае необходимо анализировать, какая именно модель распределения потока доходов учтена в использованном методе обоснования величины ставки дисконтирования и коэффициента капитализации, не возникает ли двойного учета каких-либо факторов или временного разрыва в получении потока доходов.
4. В большинстве практических примеров влияние периода дисконтирования реверсии на итоговую стоимость объекта оценки является несущественным
, меньше погрешности расчета, и может быть оценено как «менее половины ставки дисконтирования, умноженной на стоимость реверсии, приведенной к дате оценки».
Для типичных объектов коммерческой недвижимости в российских городах - милионниках, для эксплуатации которых не требуется проведение значительных строительных мероприятий, различие в итоговой величине стоимости при разных периодах дисконтирования реверсии (см. п. 2 и 3) составит около 3-4%(отметим, что это влияние на результат только одного из подходов к оценке).
Учитывая вышеизложенное, в отчетах об оценке целесообразно в явном виде указывать: модель доходного подхода подразумевает, что объект оценки будет продан в конце прогнозного периода – период дисконтирования реверсии совпадает с продолжительностью прогнозного периода.
Положения, представленные в настоящей статье, преследуют практическую цель повышения уровня усвоения учебного материала обучающихся по дисциплинам оценочного и управленческого пула, а также повышение профессионального уровня оценщиков.