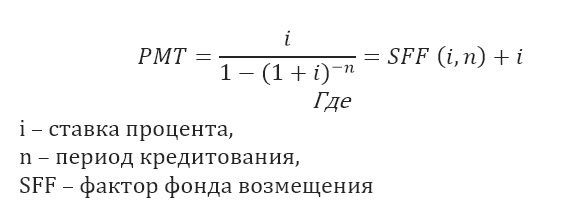Недвижимое имущество:Раздел 3. Доходный подход

Навигация по разделу "недвижимость:"общие темы, базовые понятия, доходный подход, затратный подход, сравнительный подход, оценка земельного участка, прочее, рекомендованные источники, глоссарий - недвижимость

Содержание

1 3.1. Потенциальный валовый доход
2 3.2. Действительный валовый доход
3 3.3. Операционные расходы
4 3.4. Чистый операционный доход
5 3.5. Функции сложного процента
6 3.6.Ставка дисконтирования и капитализации (метод кумулятивного построения, метод рыночной экстракции
7 3.7. Метод прямой капитализации для оценки рыночной стоимости объекта недвижимости
8 3.8. Ипотечно-инвестиционный анализ
9 3.9. Метод дисконтирования денежных потоков
10 3.10.Методы капитализации по расчетным моделям
11 3.11. Норма возврата капитала (методы Ринга, Хоскольда, Инвуда)

3.1. Потенциальный валовый доход

Потенциальный валовый доход (ПВД) – доход, который способен приносить объект при сдаче его или его элементов в аренду и получении арендной платы в полном объеме:

$LaTeX: {\cyr PVD} = AC \times N$

где:

$LaTeX: AC$ – арендная ставка, ден.ед./ед.площади/год;

$LaTeX: N$ – Количественная характеристика объекта, например, ед., кв.м.

Связь ПВД с другими уровнями дохода от эксплуатации объекта описывается следующими формулами:

$LaTeX: {\cyr PVD - NZ - NP + DX_{\tiny \cyr PR} = DVD$

$LaTeX: {\cyr DVD - OR - RZ = CHOD$

где:

$LaTeX: \cyr PVD$ – потенциальный валовый доход, ден.ед.;

$LaTeX: \cyr NZ$ – потери от недозагрузки, ден.ед.;

$LaTeX: \cyr NP$ – потери от неплатежей, ден.ед.;

$LaTeX: \cyr DX_{\tiny \cyr PR}$ – прочие доходы от нормального рыночного использования объекта недвижимости, ден.ед.;

$LaTeX: \cyr DVD$ – действительный валовый доход, ден.ед.;

$LaTeX: \cyr OP$ – операционные расходы, ден.ед.;

$LaTeX: \cyr PZ$ – расходы на замещение, ден.ед.;

$LaTeX: \cyr CHOD$ – чистый операционный доход, ден.ед..

На что обратить внимание в оценочной практике: при определении дохода от сдачи недвижимости в аренду необходимо соблюдать соответствие между ставкой аренды и базой для ее начисления. Ставке аренды за общую площадь соответствует общая площадь, за полезную площадь – полезная площадь. Полезная (арендопригодная площадь) – площадь объекта недвижимости, которая может быть сдана в аренду. Коэффициент арендопригодной площади здания – отношение площади, которую можно сдать в аренду, к общей площади здания

3.2. Действительный валовый доход

Действительный валовый доход (ДВД) – потенциальный валовый доход (ПВД) за вычетом потерь от недозагрузки, неплатежей арендаторов, а также с учетом дополнительных видов доходов.

Связь ДВД с другими уровнями дохода от эксплуатации недвижимости описывается следующими формулами:

$LaTeX: {\cyr PVD - NP - NZ + DX_{\tiny \cyr PR} = DVD$ $LaTeX: {\cyr DVD - OP - PZ = CHOD$

где:

$LaTeX: \cyr PVD$ – потенциальный валовый доход, ден.ед.;

$LaTeX: \cyr NP$ – потери от неплатежей, ден.ед.;

$LaTeX: \cyr NZ$ – потери от недозагрузки, ден.ед.;

$LaTeX: \cyr DX_{\tiny \cyr PR}$ – прочие доходы от нормального рыночного использования объекта недвижимости, ден.ед.;

$LaTeX: \cyr DVD$ – действительный валовый доход, ден.ед.;

$LaTeX: \cyr OP$ – операционные расходы, ден.ед.;

$LaTeX: \cyr PZ$ – расходы на замещение, ден.ед.;

$LaTeX: \cyr CHOD$ – чистый операционный доход, ден.ед..

На что обратить внимание в оценочной практике: при определении дохода от сдачи недвижимости в аренду необходимо соблюдать соответствие между ставкой аренды и базой для ее начисления. Ставке аренды за общую площадь соответствует общая площадь, за полезную площадь – полезная площадь.

Полезная (арендопригодная площадь) – площадь объекта недвижимости, которая может быть сдана в аренду.

Коэффициент арендопригодной площади здания – отношение площади, которую можно сдать в аренду, к общей площади здания

3.3. Операционные расходы

Постоянные расходы – не зависят от загрузки объекта недвижимости (например, арендные или страховые платежи).

Переменные расходы – зависят от загрузки объекта недвижимости (например, оплата электроэнергии, затраты на уборку и т.п.).

3.4. Чистый операционный доход

Чистый операционный доход (ЧОД) – действительный валовый доход от приносящей доход недвижимости за вычетом операционных расходов и расходов на замещение.

Связь ЧОД с другими уровнями дохода от эксплуатации недвижимости описывается следующими формулами: $LaTeX: {\cyr PVD - NP - NZ + DH_{\tiny \cyr PR} = DVD$

$LaTeX: {\cyr DVD - OP - PZ = {CH}OD$

где:

$LaTeX: \cyr PVD$ – потенциальный валовый доход, ден.ед.;

$LaTeX: \cyr NP$ – потери от неплатежей, ден.ед.;

$LaTeX: \cyr NZ$ – потери от недозагрузки, ден.ед.;

$LaTeX: \cyr DH_{\tiny \cyr PR}$ – прочие доходы от нормального рыночного использования объекта недвижимости, ден.ед.;

$LaTeX: \cyr DVD$ – действительный валовый доход, ден.ед.;

$LaTeX: \cyr OP$ – операционные расходы, ден.ед.;

$LaTeX: \cyr PZ$ – расходы на замещение, ден.ед.;

$LaTeX: \cyr CHOD$ – чистый операционный доход, ден.ед..

3.5. Функции сложного процента

3.5.1. Сложный процент – модель расчета, при которой проценты прибавляются к основной сумме [вклада] и в дальнейшем сами участвуют в создании новых процентов.

3.5.2. Шесть функций сложного процента (подразумевается, что платежи возникают в конце соответствующего периода):

Таблица 8
№ п/п	Наименование функции	Формула расчета, пример решения задачи
1	Накопленная (будущая) сумма единицы	Показывает накопление 1 ден.ед. за период: $LaTeX: FV = PV \times(1+i)^t,$ где: FV – будущая стоимость, ден. ед. PV – текущая стоимость, ден. ед. i – ставка накопления (дисконтирования), доли ед./период времени t – интервал времени, периодов времени
2	Текущая стоимость единицы	Показывает текущую стоимость 1 ден.ед., которая возникает в будущем: $LaTeX: PV = \frac{FV}{ (1+i) ^t}.$
3	Накопление единицы за период	Показывает, какой по истечении всего срока будет будущая стоимость серии аннуитетных платежей: $LaTeX: FV = \frac {(1+i)^n-1}{i}\times PMT,$ где: PMT – аннуитетный платеж, ден. ед. Аннуитетный – серия равновеликих периодических платежей.
4	Фактор фонда возмещения	Показывает величину единичного аннуитетного платежа, который необходим для того, чтобы к концу срока накопить 1 ден.ед.: $LaTeX: PMT = \frac{FV\times i}{ (1+i) ^n-1}.$
5	Текущая стоимость обычного аннуитета	Показывает величину текущей стоимости будущего аннуитетных платежей: $LaTeX: PV = PMT\times \frac{1-(1+i)^{-n}}{i}.$
6	Взнос на амортизацию единицы	Показывает величину будущего аннуитетного платежа, необходимого для полной амортизации (погашения) кредита: $LaTeX: PMT = \frac{PV \times i}{1-(1+i)^{-n}}.$

3.5.3. Зависимость между ставками накопления (дисконтирования) для различных по продолжительности периодов времени начисления:

базовый вариант:

$LaTeX: 1+i_t = {^\dfrac {T}{t}sqrt{(1+i_t)}} = {(1+i)^\dfrac{T}{t}},$

упрощенный вариант:

$LaTeX: i_t = {\frac {i_t}{(\dfrac{T}{t})},$

где:

T – бóльший по продолжительности период времени;

t – меньший по продолжительности период времени.

Таблица 9
Ставка накопления (дисконтирования)	Формула расчета из годовой ставки накопления ( $LaTeX: t_{\cyr god}$ )
Ставка накопления (дисконтирования)	Нормальный вариант	Упрощенный вариант
Месячная	$LaTeX: ^{12}sqrt{(1+i_{\cyr god})}-1 = {(1+i_{\cyr god})^\dfrac{1}{12}}-1$	$LaTeX: \frac{i_{\cyr god}}{12}$
Квартальная	$LaTeX: ^{4}sqrt{(1+i_{\cyr god})}-1 = {(1+i_{\cyr god})^\dfrac{1}{4}}-1$	$LaTeX: \frac{i_{\cyr god}}{4}$
Полугодовая	$LaTeX: ^{2}sqrt{(1+i_{\cyr god})}-1 = {(1+i_{\cyr god})^\dfrac{1}{2}}-1$	$LaTeX: \frac{i_{\cyr god}}{2}$

Упрощенный вариант используется при малых величинах ставки / невысоких требованиях к точности расчета. Например, при годовой ставке дисконтирования в размере 20% расчет величины месячной ставки по нормальному варианту даст результат в размере 1,531%, а по упрощенному – в размере 1,667%.

3.5.4. Функции 2, 4, и 6 являются обратными по отношению к 1, 3 и 5 (соответственно) – если забыта прямая, то ее можно вывести из обратной (и наоборот).

3.5.5. Примеры задач.

Задача 1. Какова текущая стоимость 1 000 000 руб., которые будут получены через 5 лет при средней величине годовой инфляции 10%? Решение:

$LaTeX: PV = \frac1{1 000 000}{(1+0,5)^5}= 620921$

При условно равномерном распределении денежных потоков в течение срока (0; t) дисконтирование осуществляется на середину периода, а общая формула преобразуется следующим образом:

$LaTeX: PV = \frac{FV}{(1+i)^{t-0,5}}.$

Задача 2. Определить текущую стоимость 1 000 000 руб., которые будут получены в течение года после даты оценки. Поступления равномерны в течение всего года, ставка дисконтирования 15% годовых. Решение: $LaTeX: PV = \frac1{1 000 000}{(1+0,15)^{0,5}}=932 505.$

При изменении величины ставки дисконтирования в течение времени (переменная ставка дисконтирования) общая формула принимает следующий вид: $LaTeX: PV=\frac{FV}{(1+t_1)^{t_1}\;\times(1+i_2\;)^{t_{2\;}}\times...\times(1+i_m\;)^{t_m}}$

где: i_m – ставка дисконтирования в интервал времени с tm доли ед./период.

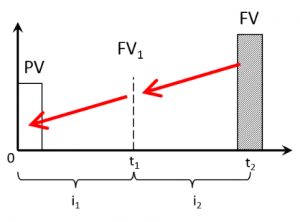
Задача 3. – определить текущую стоимость денежной суммы при следующих условиях: FV = 200 000 руб., t1 = t2 = 1 год, i1 = 15%/год, i2 = 20%/год.

Решение.

$LaTeX: PV = \frac{FV}{ (1+i_1)^{t_1} \times (1+i_1)^{t_2}}=\frac{200 000}{ (1+0,2)^1 \times (1+0,15)^1 }=144 928.$

Пояснение: процесс дисконтирования для наглядности разобьём на два этапа: приведение FV к моменту t1; приведение FV1 к моменту времени 0: $LaTeX: PV=\frac{FV}{(1+i_2)^{t_2-t_1}}= \frac{200 000}{(1+0,2)^1} = 166 667$ $LaTeX: PV=\frac{FV_1}{(1+i_1)^{t_1}}= \frac{166 667}{(1+0,15)^1} = 144 928$

3.5.6. На что обратить внимание в оценочной практике: величины ставки накопления и периода времени должны соответствовать друг другу. Месячной ставке соответствует период времени в месяцы; годовой – в годах и т.д.

3.6.Ставка дисконтирования и капитализации (метод кумулятивного построения, метод рыночной экстракции

3.6.1. Ставка дисконтирования:

процентная ставка, используемая для приведения прогнозируемых денежных потоков (доходов и расходов) к заданному моменту времени, например, к дате оценки;
процентная ставка, характеризующая требуемую инвестором доходность при инвестировании в объекты и проекты.

Синонимы – требуемая норма (ставка) доходности, норма отдачи на вложенный капитал. Размерность – проценты или доли единицы. В зависимости от учета инфляционной составляющей выделяют реальную (очищенная от инфляционной составляющей) и номинальную (без очищения) ставку дисконтирования. Взаимосвязь между ними имеет следующий вид (формула Фишера):

$LaTeX: i_p=\frac{i_{\tiny H}-i_{\tiny \cyr inf}}{1+i_{\tiny \cyr inf}}$

где:

$LaTeX: i_p$ - реальная ставка, доли ед.

$LaTeX: i_{\tiny H}$ - номинальная ставка, доли ед.;

$LaTeX: i_{\cyr inf}$ - темп инфляции, доли ед.

3.6.2. Ставка капитализации (коэффициент капитализации) – выраженное в процентах отношение чистого операционного дохода объекта к его рыночной стоимости.

3.6.3. Метод кумулятивного построения – метод расчета ставки дисконтирования, учитывающий риски, связанные с инвестированием в объекты недвижимости. Ставка дисконтирования определяется как сумма "безрисковой" доходности, премии за низкую ликвидность, премии за риск вложения в недвижимость, премии за инвестиционный менеджмент:

$LaTeX: i_{\tiny \cyr NL}=\frac{i}{12} \times N$

где:

$LaTeX: N$ - срок экспозиции объекта на рынке, мес.;

$LaTeX: i_{\tiny \cyr BR}$ - безрисковая ставка, %.

Срок экспозиции объекта недвижимости на открытом рынке (срок экспозиции) – период времени от выставления объекта на продажу до поступления денежных средств за проданный объект или типичный период времени, который необходим для того, чтобы объект был продан на открытом и конкурентном рынке при соблюдении всех рыночных условий. Премия за риск вложений (инвестиций) в объект недвижимости – премия на отраслевой риск инвестирования (инвестирование в недвижимость). Премия за инвестиционный менеджмент – премия, учитывающая сложность управления оцениваемым объектом.

3.6.4. Метод рыночной экстракции – метод определения коэффициента капитализации на основе анализа соотношения чистого арендного дохода и цен продаж по данным реальных сделок или соответствующим образом скорректированных цен предложений объектов недвижимости при условии, что существующее использование объектов соответствует их наилучшему и наиболее эффективному использованию:

$LaTeX: R=\frac{\tiny \cyr CHOD}{C}$

где:

$LaTeX: R$ - общая ставка капитализации, доли е

$LaTeX: C$ - рыночная стоимость, ден.ед.;

$LaTeX: i_{\tiny \cyr CHOD}$ - чистый операционный доход, ден.ед./год.

Результаты, полученные по различным аналогам, взвешиваются.

3.6.5. На что обратить внимание в практической деятельности: величины ставок дисконтирования и капитализации должны соответствовать типу денежного потока (например, в части учета инфляционной или налоговой составляющей).

3.7. Метод прямой капитализации для оценки рыночной стоимости объекта недвижимости

Метод прямой капитализации – частный случай метода дисконтирования денежных потоков. Применяется, когда объект оценки генерирует чистый операционный доход, величина которого либо относительно постоянна, либо изменяется равномерно (общая теория оценки). Отметим, что применительно к оценке недвижимости в п.п. «в» п. 23 ФСО №7 указано, что метод применяется для оценки объектов, не требующих значительных капитальных вложений в их ремонт или реконструкцию, фактическое использование которых соответствует их наиболее эффективному использованию.

Сущность метода:

$LaTeX: {\cyr C} = \frac{\cyr CHOD}{R}$

где:

$LaTeX: C$ – рыночная стоимость объекта оценки, ден.ед.;

$LaTeX: \cyr CHOD$ – чистый операционный доход, ден.ед./год (период);

$LaTeX: R$ – общая ставка капитализации, доли ед./год (период).

Отличие метода прямой капитализации от методов капитализации по расчетным моделям заключается в том, что:

в методах капитализации по расчетным моделям величина ставки капитализации рассчитывается на основе величины ставки дисконтирования и нормы возврата капитала, которая определяется, например, по моделям Ринга, Инвуда, Хоскольда;
в методе прямой капитализации величина ставки капитализации определяется напрямую, например, из объектов-аналогов методом рыночной экстракции.

3.8. Ипотечно-инвестиционный анализ

3.8.1. Основные определения.

3.8.1.1. Ипотечный кредит – кредит, обеспечением (залогом) по которому выступает недвижимое имущество. При получении кредита на покупку недвижимого имущества сама приобретаемая недвижимость поступает в ипотеку (залог) кредитору как гарантия возврата кредита.

Основные виды кредитов:

с постоянным платежом (самоамортизирующийся кредит) – погашение процентов и основного тела кредита осуществляется равными платежами;
с переменными платежами – погашение процентов и основного тела кредита осуществляется платежами, величина которых изменяется с течением времени под действием различных факторов (например, изменение остатка основного тела кредита или процентной ставки). Одним из вариантов кредита данного вида является кредит с шаровым платежом, погашение которого осуществляется единым платежом в конце срока.

3.8.1.2. Ипотечная постоянная – отношение ежегодных расходов по обслуживанию ипотечного кредита к первоначальной сумме (величина аннуитетного платежа, определяемого по функции «взнос на амортизацию единицы» для самоамортизирующегося кредита):

Ипотечная постоянная для самоамортизирующегося кредита рассчитывается при помощи функции сложного процента «взнос на амортизацию единицы» и равна шестой функции сложного процента
См. таблицу здесь

В случае шарового платежа ипотечная постоянная равна ставке процента по кредиту.

3.8.1.3. Эффективная ставка по кредиту – показатель, определяющий реальную стоимость кредита. Помимо номинальной процентной ставки по кредиту учитывает и все сопутствующие расходы по его обслуживанию (комиссии за открытие и ведение счета, за прием в кассу наличных денег, за получение наличности в банкомате и пр.).</p>

3.8.1.4. Коэффициент ипотечной задолженности – отношение суммы кредита к стоимости объекта недвижимости, выступающего залогом по соответствующему кредиту:

$LaTeX: {\cyr K}_{\tiny \cyr IZ}\;=\;\frac{\cyr K}C_{\tiny H} \times100\%$

где:	К_ИЗ –	коэффициент ипотечной задолженности, доли ед.;
	К –	сумма кредита, ден.ед.;
	С_Н –	стоимость объекта недвижимости, ден.ед.

3.8.2. Основной математический аппарат ипотечно-инвестиционного анализа:

3.8.3. Финансовый леверидж (применительно к ипотечно инвестиционному анализу) – соотношение ставок доходности на собственный капитал и недвижимости в целом:

положительный – R_СК > R_Н(свидетельствует об эффективном инвестировании собственного капитала);
отрицательный – R_СК<R_Н.

3.8.4. Пример задачи. Определить знак финансового левериджа при следующих условиях: ставка доходности недвижимости 15%; коэффициент ипотечной задолженности 70%; кредит получен на 20 лет под 10% годовых, в течение срока кредитования уплачиваются только проценты, тело кредита возвращается единым платежом в конце.Решение:

$LaTeX: C_H\;=\;x.$

$LaTeX: K=K_{\tiny \cyr iz}\times C_H=x\times0.7=0.7x.$ $LaTeX: CK=C_H\;-\;K\;=\;x\;-\;0.7x\;=\;0.3x.$

$LaTeX: \begin{array}{l}POK=0.1\times K=0.1\times0.7x=0.07x.\\\end{array}$

$LaTeX: \begin{array}{l}R_{CK}=\frac{{\cyr CHOD}\;-\;POK}{CK}=\frac{0.15x\;-\;0.07x}{0.3x}=0.26(6)\sim26.7\%\\\end{array}$

$LaTeX: R_{CK}\;>\;R_{H\;}\rightarrow$ леверидж положительный

3.9. Метод дисконтирования денежных потоков

Метод дисконтирования денежных потоков – метод расчета стоимости, основанный на приведении (дисконтировании) будущих денежных потоков доходов и расходов, связанных с объектом недвижимости, в том числе от его продажи в конце прогнозного периода, к дате, на которую определяется стоимость.

Дисконтирование денежных потоков – процесс определения стоимости денежных потоков на предыдущий момент (движение влево по оси времени).

Общая формула расчета имеет следующий вид (при возникновении денежных потоков в конце периода):

$LaTeX: C\;=\;\sum_{j=1}^n\frac{CF_j}{(1+i)^j}+\frac{CF_{\tiny \cyr REV}}{(1+i)^n}$

где:	С –	стоимость объекта оценки, ден. ед.;
	CF_j –	денежный поток j-ого периода, ден. ед.;
	CF_РЕВ –	реверсия, ден.ед.;
	i –	cтавка дисконтирования, доли ед.;

Дисконтный множитель (фактор (коэффициент) дисконтирования) – коэффициент, умножение на который величины денежного потока будущего периода дает его текущую стоимость:

$LaTeX: d=\;\frac1{(1+i)^t}$

где:

d –

Дисконтный множитель, доли ед.

В случае, когда период генерации денежных потоков условно бесконечен, его разделяют на:

· прогнозный период – период времени, в течение которого моделируются денежные потоки от объекта недвижимости. В качестве прогнозного периода могут рассматриваться типичный срок владения подобными активами, период до выхода объекта на стабильные потоки доходов и расходов;

· постпрогнозный период – период времени, наступающий после прогнозного периода.

Для определения денежных потоков постпрогнозного периода может быть использована модель капитализации.

Денежный поток постпрогнозного периода (реверсия) определяется с помощью следующих методов:
1. Определения цены предполагаемой продажи по истечении прогнозного периода, исходя из анализа текущего состояния рынка, из мониторинга стоимости аналогичных объектов и предположений относительно будущего состояния объекта;
2. Принятия допущений относительно изменения стоимости недвижимости за период владения;
3. Капитализации дохода за год, следующий за годом окончания прогнозного периода.

При использовании модели капитализации для определения денежных потоков постпрогнозного периода используется следующая формула расчета (при возникновении денежных потоков в конце каждого периода):

$LaTeX: PV\;=\;\sum_{j=1}^n\frac{FV_j}{(1+i)^j}+\frac{FV_{n+1}}R\times\frac1{(1+i)^n}$

где:	PV –	текущая стоимость денежных потоков прогнозного и постпрогнозного периодов, ден.ед.;
	FV_j –	денежный поток в j-ом периоде, ден. ед.;
	n–	продолжительность прогнозного периода, периодов;
	R–	ставка капитализации, доли ед.

Пример задачи. Определить текущую стоимость следующих денежных потоков. 1 год – 100 ед., 2 год – 150 ед., 3 год – 100 ед., 4 год (первый год постпрогнозного периода) – 120 ед. I = 15%, R = 20%. Дисконтирование выполнять на конец периода.

Решение:

Таблица 10.

Показатель	Значение
	Прогнозный период			Первый год постпрогнозного периода
	1 год	2 год	3 год	Первый год постпрогнозного периода
Денежный поток, ден.ед.	100	150	100	120
Период дисконтирования, лет	1	2	3	3
Ставка дисконтирования, %	15	15	15	15
Дисконтный множитель, доли ед.	0,8696	0,7561	0,6575	0,6575
Текущая стоимость, ден.ед.	87	113	66
Ставка капитализации, %				20
Будущая стоимость реверсии, ден.ед.				600
Текущая стоимость реверсии, ден.ед.	395
Текущая стоимость денежных потоков прогнозного и постпрогнозного периодов, ден.ед.	661

3.10.Методы капитализации по расчетным моделям

Метод капитализации по расчетным моделям применяется для оценки недвижимости, генерирующей регулярные потоки доходов с ожидаемой динамикой их изменения.
При этом динамика изменения может быть описана математически – как правило линейная, либо экспоненциальная (регулярное изменение на какую-либо величину, либо изменение с заданным темпом).
Капитализация таких доходов проводится по общей ставке капитализации, конструируемой на основе ставки дисконтирования, принимаемой в расчет модели возврата капитала, способов и условий финансирования, а также ожидаемых изменений доходов и стоимости недвижимости в будущем.
Общая формула капитализации по расчетным моделям:

Отличие методов капитализации по расчетным моделям от метода прямой капитализации заключается в том, что:

в методах капитализации по расчетным моделям величина ставки капитализации рассчитывается на основе величины ставки дисконтирования и нормы возврата капитала, определяемой, например, по моделям Ринга, Инвуда, Хоскольда;
в методе прямой капитализации величина ставки капитализации определяется напрямую, например, на основе данных по объектам-аналогам методом рыночной экстракции.

Норма возврата капитала (норма возврата) – величина ежегодной потери стоимости капитала за время ожидаемого периода использования объекта.
Выделяют следующие основные методы расчета величины нормы возврата капитала: Ринга, Хоскольда, Инвуда.

Метод Ринга – метод расчета нормы возврата капитала. Предусматривается возмещение инвестированного капитала равными суммами:

$LaTeX: i_{\tiny \cyr VOZVR} = \frac{1}{T} \times 100%$

где:

$LaTeX: i_{\tiny \cyr VOZVR}$ – норма возврата, %;

$LaTeX: T$ – оставшийся срок экономической жизни объекта оценки, лет.

Как правило, метод Ринга используется при периоде прогнозирования, совпадающем с оставшимся сроком экономической жизни.

Метод Хоскольда – метод расчета нормы возврата капитала. Для реинвестируемых средств предполагается получение дохода по безрисковой ставке:

$LaTeX: i_{\tiny \cyr VOZVR} = \begin{array}{l}\\\frac{i_{ \tiny \cyr BR}}{(1+i_{\tiny \cyr BR\;})^T-1}\end{array}$

где:

$LaTeX: i_{ \tiny \cyr BR}$ – безрисковая ставка доходности,

Т – период прогнозирования. Может быть равным остаточному сроку эксплуатации, либо быть меньше его.

Метод Инвуда – метод расчета нормы возврата капитала. Для реинвестируемых средств предполагается получение дохода по ставке, равной требуемой норме доходности (норме отдачи) на собственный капитал:

$LaTeX: i_{\tiny \cyr VOZVR} = \begin{array}{l}\\\frac{i}{(1+i)^T-1}\end{array}$ Т – период прогнозирования.

Модели Хоскольда и Инвуда содержат в качестве нормы возврата на капитал фактор фонда возмещения (SFF).
В модели Хоскольда используется безрисковая ставка, в модели Инвуда – ставка дисконтирования.

Пример задачи. Определить рыночную стоимость объекта оценки методом капитализации по расчетной модели при следующих условиях: ЧОД = 100 000 ден.ед., i = 15%, оставшийся срок экономической жизни 10 лет, норму возврата определить по модели Инвуда. Решение:

$LaTeX: i{\tiny \cyr VOZVR} = \frac{ \cyr CHOD}{R} = \frac{ \cyr CHOD}{i+i{\tiny \cyr VOZVR}}$

$LaTeX: i{\tiny \cyr VOZVR} = \frac{0,15}{(1+0,15)^T-1} \approx 0,05.$

$LaTeX: PV = \frac{CHOD}{i{\tiny \cyr VOZVR}} = \frac{100 000}{0,15+0,05} = \frac{100 000}{0,2} = 500 000$
Следует отметить, что приведенные простые модели описывают идеальный случай постоянного чистого операционного дохода.
Для учета регулярно изменяющихся доходов модели корректируются.

Более подробно о расчетных моделях – см., например, С.В. Грибовский Е.Н. Иванова, Д.С. Львов, О.Е. Медведева «ОЦЕНКА СТОИМОСТИНЕДВИЖИМОСТИ», стр. 170, М, Интерреклама, 2003 и др.

3.11. Норма возврата капитала (методы Ринга, Хоскольда, Инвуда)

Норма возврата капитала (норма возврата) – величина ежегодной потери стоимости капитала за время ожидаемого периода использования объекта. Выделяют следующие основные методы расчета величины нормы возврата капитала: Ринга, Хоскольда, Инвуда.

Метод Ринга – метод расчета нормы возврата капитала. Предусматривается возмещение инвестированного капитала равными суммами:

$LaTeX: i_{\tiny \cyr VOZVR} = \frac{1}{T} \times 100%$

где:

$LaTeX: i_{\tiny \cyr VOZVR}$ – норма возврата, %;

$LaTeX: T$ – оставшийся срок экономической жизни объекта оценки, лет.

Метод Хоскольда – метод расчета нормы возврата капитала. Для реинвестируемых средств предполагается получение дохода по безрисковой ставке:

$LaTeX: i_{\tiny \cyr VOZVR} = \begin{array}{l}\\\frac{i_{ \tiny \cyr BR}}{(1+i_{\tiny \cyr BR\;})^T-1}\end{array}$

где:

$LaTeX: i_{ \tiny \cyr BR}$ – безрисковая ставка доходности.

Метод Инвуда – метод расчета нормы возврата капитала. Для реинвестируемых средств предполагается получение дохода по ставке, равной требуемой норме доходности (норме отдачи) на собственный капитал:

$LaTeX: i_{\tiny \cyr VOZVR} = \begin{array}{l}\\\frac{i}{(1+i)^T-1}\end{array}$

Пример задачи. Определить рыночную стоимость объекта оценки методом капитализации по расчетной модели при следующих условиях: ЧОД = 100 000 ден.ед., i = 15%, срок экономической жизни 10 лет, норму возврата определить по модели Инвуда. Решение:

$LaTeX: i{\tiny \cyr VOZVR} = \frac{ \cyr CHOD}{R} = \frac{ \cyr CHOD}{i+i{\tiny \cyr VOZVR}}$

$LaTeX: i{\tiny \cyr VOZVR} = \frac{0,15}{(1+0,15)^T-1} \approx 0,05.$

$LaTeX: PV = \frac{CHOD}{i{\tiny \cyr VOZVR}} = \frac{100 000}{0,15+0,05} = \frac{100 000}{0,2} = 500 000$

Навигация по разделу "недвижимость:"общие темы, базовые понятия, доходный подход, затратный подход, сравнительный подход, оценка земельного участка, прочее, рекомендованные источники, глоссарий - недвижимость

Недвижимое имущество:Раздел 3. Доходный подход

Содержание

3.1. Потенциальный валовый доход

3.2. Действительный валовый доход

3.3. Операционные расходы

3.4. Чистый операционный доход

3.5. Функции сложного процента

3.6.Ставка дисконтирования и капитализации (метод кумулятивного построения, метод рыночной экстракции

3.7. Метод прямой капитализации для оценки рыночной стоимости объекта недвижимости

3.8. Ипотечно-инвестиционный анализ

3.9. Метод дисконтирования денежных потоков

3.10.Методы капитализации по расчетным моделям

3.11. Норма возврата капитала (методы Ринга, Хоскольда, Инвуда)

Навигация

Персональные инструменты

Пространства имён

Варианты

Просмотры

Ещё

Поиск

Навигация

Квалэкзамен

Материалы

Инструменты