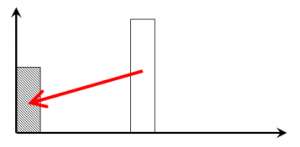
7.2. Функции сложного процента и дисконтирование
Общая формула дисконтирования на конец периода\[ PV = \frac1{FV}{(1+i)^t}= FV \times \left[\frac1{(1+t)^t}\right] \]
- где:
- \[ FV \] – будущая стоимость, ден. ед.;
- \[ PV \] – текущая стоимость, ден. ед.;
- \[ i \] – ставка дисконтирования, доли ед./период времени;
- \[ t \] – интервал времени с даты оценки до даты возникновения FV, периодов времени.
Дробь в квадратных скобках – дисконтный множитель (коэффициент дисконтирования) – показывает соотношение текущей и будущей стоимостями денежного потока; коэффициент, умножение на который величины денежного потока будущего периода дает его текущую стоимость.
Задача 1. Какова текущая стоимость 1 000 000 руб., которые будут получены через 5 лет при средней величине годовой инфляции 10%? Решение\[ PV = \frac1{1 000 000}{(1+0,1)^5}= 620921 \]
При условно равномерном распределении денежных потоков в течение срока (0; t) дисконтирование осуществляется на середину периода, а общая формула преобразуется следующим образом\[ PV = \frac{FV}{(1+i)^{t-0,5}}. \]
Задача 2. Определить текущую стоимость 1 000 000 руб., которые будут получены в течение года после даты оценки. Поступления равномерны в течение всего года, ставка дисконтирования 15% годовых. Решение\[ PV = \frac1{1 000 000}{(1+0,15)^{0,5}}=932 505. \]
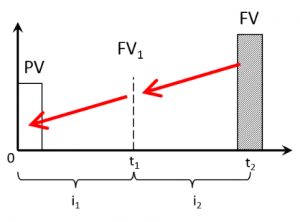
При изменении величины ставки дисконтирования в течение времени (переменная ставка дисконтирования) общая формула принимает следующий вид\[ PV=\frac{FV}{(1+t_1)^{t_1}\;\times(1+i_2\;)^{t_{2\;}}\times...\times(1+i_m\;)^{t_m}} \]
где: im – ставка дисконтирования в интервал времени с tm доли ед./период.
Задача 3. – определить текущую стоимость денежной суммы при следующих условиях: FV = 200 000 руб., t1 = t2 = 1 год, i1 = 15%/год, i2 = 20%/год.
Решение.
\( PV = \frac{FV}{ (1+i_1)^{t_1} \times (1+i_1)^{t_2}}=\frac{200 000}{ (1+0,2)^1 \times (1+0,15)^1 }=144 928. \)
Пояснение: процесс дисконтирования для наглядности разобьём на два этапа: приведение FV к моменту t1; приведение FV1 к моменту времени 0\[ PV=\frac{FV}{(1+i_2)^{t_2-t_1}}= \frac{200 000}{(1+0,2)^1} = 166 667 \] \( PV=\frac{FV_1}{(1+i_1)^{t_1}}= \frac{166 667}{(1+0,15)^1} = 144 928 \)